코딩테스트 22일차
저주의 숫자 3
3x 마을 사람들은 3을 저주의 숫자라고 생각하기 때문에 3의 배수와 숫자 3을 사용하지 않습니다. 3x 마을 사람들의 숫자는 다음과 같습니다.
function solution(n) {
let arr = [];
let num = 0;
while (arr.length !== n && ++num) if (num%3!==0 && !(''+num).includes('3')) arr.push(num);
return arr.pop();
}✏️풀이
let arr = [];: 빈 배열 arr을 선언합니다. 이 배열은 조건을 만족하는 수열의 요소들을 저장할 것입니다.
let num = 0;: 변수 num을 0으로 초기화합니다. 이 변수는 수열을 생성하는 데 사용될 숫자입니다.
while (arr.length !== n && ++num): arr의 길이가 n과 같지 않은 동안 루프를 실행합니다. ++num은 num의 값을 1씩 증가시키는 것을 의미합니다. 이 부분에서 num을 증가시키면서 수열을 생성합니다.
if (num%3!==0 && !(''+num).includes('3')): 만약 num이 3으로 나누어 떨어지지 않고, 문자열로 변환한 후에 '3'을 포함하지 않는다면, 아래의 코드를 실행합니다.
num%3!==0: num을 3으로 나눈 나머지가 0이 아니라는 것은 3의 배수가 아님을 의미합니다.
!(''+num).includes('3'): num을 문자열로 변환한 후에 '3'을 포함하지 않는다는 것은 num에 숫자 3이 포함되지 않음을 의미합니다.
arr.push(num);: 조건을 만족하는 경우, arr 배열에 num을 추가합니다.
return arr.pop();: 반복문이 종료된 후에, arr 배열의 마지막 요소를 반환합니다.
평행
점 네 개의 좌표를 담은 이차원 배열 dots가 다음과 같이 매개변수로 주어집니다.
[[x1, y1], [x2, y2], [x3, y3], [x4, y4]]
주어진 네 개의 점을 두 개씩 이었을 때, 두 직선이 평행이 되는 경우가 있으면 1을 없으면 0을 return 하도록 solution 함수를 완성해보세요.
function solution(dots) {
for (let i = 0; i < 3; i++) {
const [x1, y1] = dots[i];
for (let j = i + 1; j < 4; j++) {
const [x2, y2] = dots[j];
const slope = (y2 - y1) / (x2 - x1);
let parallel = true;
for (let k = 0; k < 4; k++) {
if (k !== i && k !== j) {
const [x3, y3] = dots[k];
for (let l = k + 1; l < 4; l++) {
if (l !== i && l !== j) {
const [x4, y4] = dots[l];
const currentSlope = (y4 - y3) / (x4 - x3);
if (slope !== currentSlope) {
parallel = false;
break;
}
}
}
}
if (!parallel) break;
}
if (parallel) return 1;
}
}
return 0;
}✏️풀이
첫 번째 반복문은 첫 번째 점부터 세 번째 점까지를 선택합니다. 이를 위해 변수 i를 0부터 2까지 반복합니다.
dots[i]에서 첫 번째 점의 좌표인 [x1, y1]을 추출합니다.
두 번째 반복문은 i 다음의 인덱스부터 마지막 점까지를 선택합니다. 이를 위해 변수 j를 i + 1부터 3까지 반복합니다.
dots[j]에서 두 번째 점의 좌표인 [x2, y2]을 추출합니다.
선택한 두 점을 이은 직선의 기울기인 slope를 계산합니다. 기울기는 (y2 - y1) / (x2 - x1)로 구할 수 있습니다.
parallel 변수를 true로 초기화합니다. 이 변수는 현재 선택한 두 직선이 평행한지를 나타내는 플래그 역할을 합니다.
내부 반복문은 네 개의 점을 모두 확인합니다. 이를 위해 변수 k를 0부터 3까지 반복합니다.
k가 i와 j와 같지 않을 때, 즉 현재 선택한 네 번째 점이 아닐 때에만 실행됩니다.
dots[k]에서 세 번째 점의 좌표인 [x3, y3]을 추출합니다.
두 번째 내부 반복문은 k 다음의 인덱스부터 마지막 점까지를 선택합니다. 이를 위해 변수 l를 k + 1부터 3까지 반복합니다.
l이 i와 j와 같지 않을 때, 즉 현재 선택한 다섯 번째 점이 아닐 때에만 실행됩니다.
dots[l]에서 네 번째 점의 좌표인 [x4, y4]을 추출합니다.
선택한 네 개의 점을 이은 직선의 기울기인 currentSlope를 계산합니다.
slope와 currentSlope를 비교하여 기울기가 다른 경우, 즉 두 직선이 평행하지 않은 경우 parallel을 false로 설정하고 내부 반복문을 종료합니다.
내부 반복문 종료 후, parallel이 true인 경우는 모든 네 개의 점에 대해 기울기가 동일한 경우를 의미합니다. 이 경우 1을 반환하여 두 직선이 평행함을 나타냅니다.
외부 반복문이 모두 종료된 경우, 즉 모든 직선 쌍에 대해 평행 여부를 확인한 후에도 평행한 직선이 없는 경우 0을 반환합니다
겹치는 선분의 길이
선분 3개가 평행하게 놓여 있습니다. 세 선분의 시작과 끝 좌표가 [[start, end], [start, end], [start, end]] 형태로 들어있는 2차원 배열 lines가 매개변수로 주어질 때, 두 개 이상의 선분이 겹치는 부분의 길이를 return 하도록 solution 함수를 완성해보세요.
lines가 [[0, 2], [-3, -1], [-2, 1]]일 때 그림으로 나타내면 다음과 같습니다.
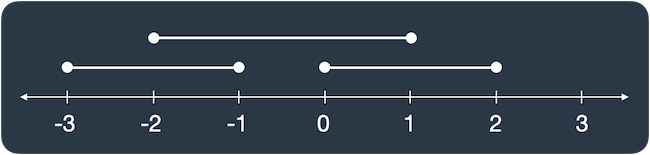
선분이 두 개 이상 겹친 곳은 [-2, -1], [0, 1]로 길이 2만큼 겹쳐있습니다.
function solution(lines) {
let line = new Array(200).fill(0);
lines.forEach(([a, b]) => {
for(; a < b; a++) line[a+100]++;
});
return line.reduce((a, c) => c > 1 ? a + 1 : a, 0)
}✏️풀이
let line = new Array(200).fill(0);: 길이가 200이고 0으로 초기화된 배열 line을 생성합니다. 이 배열은 선분이 겹치는 위치의 개수를 저장할 것입니다.
lines.forEach(([a, b]) => { ... }): lines 배열의 각 요소에 대해 반복문을 실행합니다. 각 요소는 [a, b] 형태의 배열이며, a와 b는 선분의 시작과 끝을 나타냅니다.
for(; a < b; a++) line[a+100]++;: a부터 b-1까지 반복문을 실행하며, line 배열에서 해당 위치의 값을 1씩 증가시킵니다. 이 때, a+100을 인덱스로 사용하는 이유는 음수 인덱스를 피하기 위함입니다. 따라서, a와 b는 -100부터 99까지의 범위에 대응됩니다.
return line.reduce((a, c) => c > 1 ? a + 1 : a, 0): line 배열을 순회하면서 값이 1보다 큰 경우를 카운트하여 반환합니다. reduce() 메서드는 누적된 값을 계산하기 위해 사용되며, 콜백 함수는 각 요소마다 실행됩니다. 요소 c가 1보다 큰 경우에만 a를 1 증가시키고, 그렇지 않은 경우에는 그대로 반환합니다. 초기값으로 0을 사용하여 계산을 시작합니다.
유한소수 판별하기
소수점 아래 숫자가 계속되지 않고 유한개인 소수를 유한소수라고 합니다. 분수를 소수로 고칠 때 유한소수로 나타낼 수 있는 분수인지 판별하려고 합니다. 유한소수가 되기 위한 분수의 조건은 다음과 같습니다.
기약분수로 나타내었을 때, 분모의 소인수가 2와 5만 존재해야 합니다.
두 정수 a와 b가 매개변수로 주어질 때, a/b가 유한소수이면 1을, 무한소수라면 2를 return하도록 solution 함수를 완성해주세요.
function solution(a, b) {
// 최대공약수 구하기
const gcd = getGCD(a, b);
// 약분하기
a /= gcd;
b /= gcd;
// 분모 소인수분해
while (b % 2 === 0) {
b /= 2;
}
while (b % 5 === 0) {
b /= 5;
}
// 유한소수인지 판별
if (b === 1) {
return 1;
} else {
return 2;
}
}
// 최대공약수 구하는 함수
function getGCD(a, b) {
if (b === 0) {
return a;
}
return getGCD(b, a % b);
}✏️풀이
solution 함수는 매개변수로 정수 a와 b를 받습니다.
getGCD 함수를 호출하여 a와 b의 최대공약수를 구합니다. getGCD 함수는 재귀적으로 구현되어 있으며, 유클리드 호제법을 사용하여 최대공약수를 계산합니다.
구한 최대공약수를 사용하여 a와 b를 약분합니다. 약분은 a와 b를 최대공약수로 나누어주는 것을 의미합니다.
약분한 a와 b의 분모 b를 소인수분해합니다. while 문을 사용하여 b를 2와 5로 반복적으로 나누어 소인수분해합니다.
소인수분해한 결과로 b를 확인합니다. b가 1인 경우는 분모에 2와 5 이외의 소인수가 없는 경우이므로, 유한소수입니다. 따라서 1을 반환합니다. 그렇지 않은 경우는 2와 5 이외의 소인수가 존재하는 경우이므로, 무한소수입니다. 따라서 2를 반환합니다.
코딩테스트 22일차
저주의 숫자 3
3x 마을 사람들은 3을 저주의 숫자라고 생각하기 때문에 3의 배수와 숫자 3을 사용하지 않습니다. 3x 마을 사람들의 숫자는 다음과 같습니다.
function solution(n) {
let arr = [];
let num = 0;
while (arr.length !== n && ++num) if (num%3!==0 && !(''+num).includes('3')) arr.push(num);
return arr.pop();
}✏️풀이
let arr = [];: 빈 배열 arr을 선언합니다. 이 배열은 조건을 만족하는 수열의 요소들을 저장할 것입니다.
let num = 0;: 변수 num을 0으로 초기화합니다. 이 변수는 수열을 생성하는 데 사용될 숫자입니다.
while (arr.length !== n && ++num): arr의 길이가 n과 같지 않은 동안 루프를 실행합니다. ++num은 num의 값을 1씩 증가시키는 것을 의미합니다. 이 부분에서 num을 증가시키면서 수열을 생성합니다.
if (num%3!==0 && !(''+num).includes('3')): 만약 num이 3으로 나누어 떨어지지 않고, 문자열로 변환한 후에 '3'을 포함하지 않는다면, 아래의 코드를 실행합니다.
num%3!==0: num을 3으로 나눈 나머지가 0이 아니라는 것은 3의 배수가 아님을 의미합니다.
!(''+num).includes('3'): num을 문자열로 변환한 후에 '3'을 포함하지 않는다는 것은 num에 숫자 3이 포함되지 않음을 의미합니다.
arr.push(num);: 조건을 만족하는 경우, arr 배열에 num을 추가합니다.
return arr.pop();: 반복문이 종료된 후에, arr 배열의 마지막 요소를 반환합니다.
평행
점 네 개의 좌표를 담은 이차원 배열 dots가 다음과 같이 매개변수로 주어집니다.
[[x1, y1], [x2, y2], [x3, y3], [x4, y4]]
주어진 네 개의 점을 두 개씩 이었을 때, 두 직선이 평행이 되는 경우가 있으면 1을 없으면 0을 return 하도록 solution 함수를 완성해보세요.
function solution(dots) {
for (let i = 0; i < 3; i++) {
const [x1, y1] = dots[i];
for (let j = i + 1; j < 4; j++) {
const [x2, y2] = dots[j];
const slope = (y2 - y1) / (x2 - x1);
let parallel = true;
for (let k = 0; k < 4; k++) {
if (k !== i && k !== j) {
const [x3, y3] = dots[k];
for (let l = k + 1; l < 4; l++) {
if (l !== i && l !== j) {
const [x4, y4] = dots[l];
const currentSlope = (y4 - y3) / (x4 - x3);
if (slope !== currentSlope) {
parallel = false;
break;
}
}
}
}
if (!parallel) break;
}
if (parallel) return 1;
}
}
return 0;
}✏️풀이
첫 번째 반복문은 첫 번째 점부터 세 번째 점까지를 선택합니다. 이를 위해 변수 i를 0부터 2까지 반복합니다.
dots[i]에서 첫 번째 점의 좌표인 [x1, y1]을 추출합니다.
두 번째 반복문은 i 다음의 인덱스부터 마지막 점까지를 선택합니다. 이를 위해 변수 j를 i + 1부터 3까지 반복합니다.
dots[j]에서 두 번째 점의 좌표인 [x2, y2]을 추출합니다.
선택한 두 점을 이은 직선의 기울기인 slope를 계산합니다. 기울기는 (y2 - y1) / (x2 - x1)로 구할 수 있습니다.
parallel 변수를 true로 초기화합니다. 이 변수는 현재 선택한 두 직선이 평행한지를 나타내는 플래그 역할을 합니다.
내부 반복문은 네 개의 점을 모두 확인합니다. 이를 위해 변수 k를 0부터 3까지 반복합니다.
k가 i와 j와 같지 않을 때, 즉 현재 선택한 네 번째 점이 아닐 때에만 실행됩니다.
dots[k]에서 세 번째 점의 좌표인 [x3, y3]을 추출합니다.
두 번째 내부 반복문은 k 다음의 인덱스부터 마지막 점까지를 선택합니다. 이를 위해 변수 l를 k + 1부터 3까지 반복합니다.
l이 i와 j와 같지 않을 때, 즉 현재 선택한 다섯 번째 점이 아닐 때에만 실행됩니다.
dots[l]에서 네 번째 점의 좌표인 [x4, y4]을 추출합니다.
선택한 네 개의 점을 이은 직선의 기울기인 currentSlope를 계산합니다.
slope와 currentSlope를 비교하여 기울기가 다른 경우, 즉 두 직선이 평행하지 않은 경우 parallel을 false로 설정하고 내부 반복문을 종료합니다.
내부 반복문 종료 후, parallel이 true인 경우는 모든 네 개의 점에 대해 기울기가 동일한 경우를 의미합니다. 이 경우 1을 반환하여 두 직선이 평행함을 나타냅니다.
외부 반복문이 모두 종료된 경우, 즉 모든 직선 쌍에 대해 평행 여부를 확인한 후에도 평행한 직선이 없는 경우 0을 반환합니다
겹치는 선분의 길이
선분 3개가 평행하게 놓여 있습니다. 세 선분의 시작과 끝 좌표가 [[start, end], [start, end], [start, end]] 형태로 들어있는 2차원 배열 lines가 매개변수로 주어질 때, 두 개 이상의 선분이 겹치는 부분의 길이를 return 하도록 solution 함수를 완성해보세요.
lines가 [[0, 2], [-3, -1], [-2, 1]]일 때 그림으로 나타내면 다음과 같습니다.

선분이 두 개 이상 겹친 곳은 [-2, -1], [0, 1]로 길이 2만큼 겹쳐있습니다.
function solution(lines) {
let line = new Array(200).fill(0);
lines.forEach(([a, b]) => {
for(; a < b; a++) line[a+100]++;
});
return line.reduce((a, c) => c > 1 ? a + 1 : a, 0)
}✏️풀이
let line = new Array(200).fill(0);: 길이가 200이고 0으로 초기화된 배열 line을 생성합니다. 이 배열은 선분이 겹치는 위치의 개수를 저장할 것입니다.
lines.forEach(([a, b]) => { ... }): lines 배열의 각 요소에 대해 반복문을 실행합니다. 각 요소는 [a, b] 형태의 배열이며, a와 b는 선분의 시작과 끝을 나타냅니다.
for(; a < b; a++) line[a+100]++;: a부터 b-1까지 반복문을 실행하며, line 배열에서 해당 위치의 값을 1씩 증가시킵니다. 이 때, a+100을 인덱스로 사용하는 이유는 음수 인덱스를 피하기 위함입니다. 따라서, a와 b는 -100부터 99까지의 범위에 대응됩니다.
return line.reduce((a, c) => c > 1 ? a + 1 : a, 0): line 배열을 순회하면서 값이 1보다 큰 경우를 카운트하여 반환합니다. reduce() 메서드는 누적된 값을 계산하기 위해 사용되며, 콜백 함수는 각 요소마다 실행됩니다. 요소 c가 1보다 큰 경우에만 a를 1 증가시키고, 그렇지 않은 경우에는 그대로 반환합니다. 초기값으로 0을 사용하여 계산을 시작합니다.
유한소수 판별하기
소수점 아래 숫자가 계속되지 않고 유한개인 소수를 유한소수라고 합니다. 분수를 소수로 고칠 때 유한소수로 나타낼 수 있는 분수인지 판별하려고 합니다. 유한소수가 되기 위한 분수의 조건은 다음과 같습니다.
기약분수로 나타내었을 때, 분모의 소인수가 2와 5만 존재해야 합니다.
두 정수 a와 b가 매개변수로 주어질 때, a/b가 유한소수이면 1을, 무한소수라면 2를 return하도록 solution 함수를 완성해주세요.
function solution(a, b) {
// 최대공약수 구하기
const gcd = getGCD(a, b);
// 약분하기
a /= gcd;
b /= gcd;
// 분모 소인수분해
while (b % 2 === 0) {
b /= 2;
}
while (b % 5 === 0) {
b /= 5;
}
// 유한소수인지 판별
if (b === 1) {
return 1;
} else {
return 2;
}
}
// 최대공약수 구하는 함수
function getGCD(a, b) {
if (b === 0) {
return a;
}
return getGCD(b, a % b);
}✏️풀이
solution 함수는 매개변수로 정수 a와 b를 받습니다.
getGCD 함수를 호출하여 a와 b의 최대공약수를 구합니다. getGCD 함수는 재귀적으로 구현되어 있으며, 유클리드 호제법을 사용하여 최대공약수를 계산합니다.
구한 최대공약수를 사용하여 a와 b를 약분합니다. 약분은 a와 b를 최대공약수로 나누어주는 것을 의미합니다.
약분한 a와 b의 분모 b를 소인수분해합니다. while 문을 사용하여 b를 2와 5로 반복적으로 나누어 소인수분해합니다.
소인수분해한 결과로 b를 확인합니다. b가 1인 경우는 분모에 2와 5 이외의 소인수가 없는 경우이므로, 유한소수입니다. 따라서 1을 반환합니다. 그렇지 않은 경우는 2와 5 이외의 소인수가 존재하는 경우이므로, 무한소수입니다. 따라서 2를 반환합니다.
